ORB-SLAM3 IMU preintegration code review (2)

날짜
2025/01/12
4 more properties

소개

지난 시간에 우리는 ORB-SLAM3에서 IMU preintegration의 여러 구성요소 중에 첫번째로 IMU 센서 측정 값 integration 부분을 논문과 코드를 대조하여 분석해보았습니다. 측정값 integration 부분에서는 (1) 두 키프레임 사이의 상대적인 상태 (회전, 이동, 속도) 값을 계산하고, (2) 노이즈 전파를 통해 공분산 행렬을 구하고, (3) 바이어스 업데이트를 위한 자코비안 행렬을 계산합니다. 여기서 계산된 값들은 나중에 키프레임들을 이용한 Bundle adjustment를 수행할 때나, 카메라 프레임 하나에 대한 Pose estimation등 비선형 최적화를 수행할때 사용됩니다.
이번 시간에는 비선형 최적화를 수행할때 구성하는 IMU factor의 Residual 함수와 Jacobian 행렬의 정의에 대해서 ORB-SLAM3 코드에서는 어떻게 구현되어 있는지 분석해보도록 하겠습니다.

사전 지식

Factor Graphs and MAP Esimation

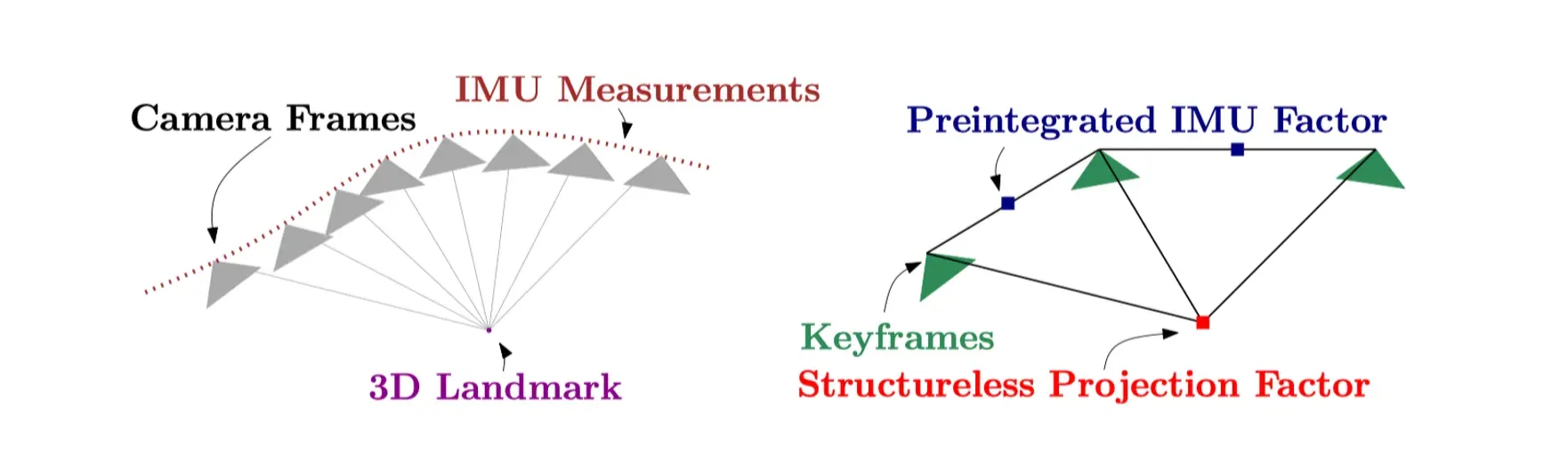
Factor graph는 확률 모델에서 변수 간의 관계를 표현하고 모든 제약조건(factor)을 만족시키는 해를 찾는데 사용되는 구조입니다. 여기서는 Visual-Inertial Odometry(VIO) 문제를 다루기 위해 사용되며 아래의 주요 구성 요소로 이루어져 있습니다.
1.
그래프 노드(Graph node)
a.
변수(Variable) 노드: 시스템의 상태값(state, Xk\mathcal{X}_k)를 나타냅니다
b.
팩터(Factor) 노드: 측정값(measurement, Zk\mathcal{Z}_k) 및 상태 간의 관계를 나타내는 확률적 요인을 나타냅니다.
2.
그래프 엣지(Graph edge)
a.
변수와 팩터를 연결하며, 어떤 변수가 어떤 팩터에 영향을 미치는가에 대한 제약조건을 나타냅니다.
IMU preintegration 논문에서 정의한 VIO 문제는 수식 (25)에서 아래와 같이 표현됩니다.
p(Xk∣Zk)∝p(X0)p(Zk∣Xk)=(a)p(X0)∏(i,j)∈Kkp(Ci,Iij∣Xk)=(b)p(X0)∏(i,j)∈Kkp(Iij∣xi,xj)∏i∈Kk∏l∈Cip(zil∣xi). \begin{equation} \begin{aligned} p(\mathcal{X}_k \mid \mathcal{Z}_k) &\propto p(\mathcal{X}_0) p(\mathcal{Z}_k \mid \mathcal{X}_k) \\ &\overset{(a)}{=} p(\mathcal{X}_0) \prod_{(i,j) \in \mathcal{K}_k} p(\mathcal{C}_i, \mathcal{I}_{ij} \mid \mathcal{X}_k) \\ &\overset{(b)}{=} p(\mathcal{X}_0) \prod_{(i,j) \in \mathcal{K}_k} p(\mathcal{I}_{ij} \mid \mathbf{x}_i, \mathbf{x}_j) \prod_{i \in \mathcal{K}_k} \prod_{l \in \mathcal{C}_i} p(\mathbf{z}_{il} \mid \mathbf{x}_i). \end{aligned} \tag{25} \end{equation}
여기서 상태값 Xk\mathcal{X}_k는 우리가 구하고자 하는 키프레임에 대한 상태(회전 Ri\mathbf{R}_i, 이동 pi\mathbf{p}_i, 속도 vi\mathbf{v}_i, 바이어스 bi\mathbf{b}_i )값을 포함하고 측정값 Zk\mathcal{Z}_k는 카메라 센서로부터의 관찰(3D 랜드마크에 대한 2D 키포인트 위치정보 Ci\mathcal{C_i})값 및 IMU 센서로부터의 측정(가속도 및 각속도 Iij\mathcal{I_{ij}})값을 포함합니다. Notation에 대해서 더 자세히 알고싶으신 분들은 논문에서 IV. Maximum a Posteriori Visual-Inertial State Estimation 섹션을 참고해주세요.
Xk≐{xi}i∈Kk, where xi≐[Ri,pi,vi,bi]Zk≐{Ci,Iij}(i,j)∈Kk.\begin{align*} \mathcal{X}_k &\doteq \left\{ \mathbf{x}_i \right\}_{i \in \mathcal{K}_k}, \text{ where } \mathbf{x}_i \doteq \left[ \mathbf{R}_i, \mathbf{p}_i, \mathbf{v}_i, \mathbf{b}_i \right] \\ \mathcal{Z}_k &\doteq \left\{ C_i, \mathcal{I}_{ij} \right\}_{(i,j) \in \mathcal{K}_k}. \end{align*}
우리는 수식 (25)의 확률모델이 최대값을 가지도록 만드는 상태값 Xk\mathcal{X}_k을 구하기 위해 Maximum-a-Priori(MAP) estimation을 수행하고자 합니다. 이를 위해 수식 (25)에 negative log를 취하여 아래와 같이 합의 형태로 표현합니다.
Xk∗≐arg⁡min⁡Xk−log⁡e p(Xk∣Zk)=arg⁡min⁡Xk∥r0∥Σ02+∑(i,j)∈Kk∥rIij∥Σij2+∑i∈Kk∑l∈Ci∥rCil∥ΣC2.(26) \begin{aligned} \boldsymbol{\mathcal{X}}_k^* &\doteq\arg\min_{\boldsymbol{\mathcal{X}}_k} -\log_e \, p(\boldsymbol{\mathcal{X}}_k \mid \boldsymbol{\mathcal{Z}}_k) \\ &= \arg\min_{\boldsymbol{\mathcal{X}}_k} \|\mathbf{r}_0\|^2_{\boldsymbol{\Sigma}_0} + \sum_{(i,j) \in \mathcal{K}_k} \|\mathbf{r}_{\mathcal{I}_{ij}}\|^2_{\boldsymbol{\Sigma}_{ij}} + \sum_{i \in \mathcal{K}_k} \sum_{l \in \mathcal{C}_i} \|\mathbf{r}_{\mathcal{C}_{il}}\|^2_{\boldsymbol{\Sigma}_C}. \end{aligned} \tag{26}
여기서 r0,rIij,rCil\mathbf{r}_0, \mathbf{r}_{\mathcal{I}_{ij}}, \mathbf{r}_{\mathcal{C}_{il}}는 각각 prior factor에 대한 residual(잔차), IMU 센서에 대한 residual, 그리고 Camera 센서에 대한 residual이 됩니다. 여기서 residual이란 센서로부터의 측정값과 상태에 대한 예측값 사이의 차이를 의미합니다. 이렇게 residual 함수로 구성된 수식 (26)을 최소값으로 만드는 파라미터 Xk\mathcal{X}_k를 찾으면 확률모델 수식 (25)의 해가 되며, 이렇게 해를 찾는 것을 시스템의 상태 추정(State estimation)이라고 합니다.

Nonlinear optimization & Open-source libraries

해를 찾는 과정은 일반적으로 비선형 최적화(Nonlinear optimization) 방법을 사용하며, 일반적인 개발자 및 공학자들이 간편하게 사용할 수 있도록 아래와 같이 많은 오픈소스 라이브러리들이 공개되어 있습니다.
•
Google, ceres-solver (http://ceres-solver.org/)
•
Georgia Tech, GTSAM (https://gtsam.org/)
•
University of Freiburg, g2o (https://github.com/RainerKuemmerle/g2o)
•
Skydio, Symforce (https://symforce.org/)
본 글에서 참고하고 있는 ORB-SLAM3 코드에서는 g2o 라이브러리를 이용해서 비선형 최적화를 수행하고 있으므로 아래에서는 g2o기준으로 코드 설명을 진행하도록 하겠습니다. 일반적인 비선형 최적화 과정에서 필요한 도구들은(예: 최적화 루프, 비선형 솔버 등)은 라이브러리에 다 구현이 되어 있으나, 우리가 풀고자 하는 문제의 시스템 모델 자체는 우리가 직접 구현해주어야 합니다. 따라서 IMU preintegration 문제에 대한 시스템 모델을 코드로 구현하는 것이 필요하며 이 때 필요한 것은 Residual 함수에 대한 정의와 Jacobian 행렬의 정의입니다. 따라서 아래의 코드 분석 섹션에서는 ORB-SLAM3의 코드와 IMU integration 논문의 수식을 대조해보면서 어떻게 구현되어 있는지 자세히 살펴보도록 하겠습니다.
혹시나 비선형 최적화 이론에 대해서 익숙하지 않으신 분들은 제가 집필한 NVIDIA Jetson Nano와 함께하는 SLAM의 이해와 구현에서 03. 비선형 최적화 이론(Non-linear optimization theorem) 부분을 살펴보시면 조금이나마 도움이 되실것 같습니다 :-)

코드 분석

Residual 함수 정의

앞에서도 잠깐 설명했지만 Residual 함수는 센서로부터의 측정값과 상태에 대한 예측값 사이의 차이를 의미합니다. 이 Residual 값이 최소가 되는 시스템의 상태를 비선형 최적화를 이용해 계산합니다. 논문에서 정의된 IMU preintegration에 대한 Residual 함수는 수식 (45)에서 설명되어있습니다. 순서대로 회전 파라미터에 대한 잔차 rΔRij\mathbf{r}_{\Delta R_{ij}}, 속도 파라미터에 대한 잔차 rΔvij\mathbf{r}_{\Delta \mathbf{v}_{ij}}, 그리고 이동 파라미터에 대한 잔차 rΔpij\mathbf{r}_{\Delta \mathbf{p}_{ij}}를 나타냅니다.
rΔRij≐Log((ΔR~ij(bˉig)Exp(∂ΔRˉij∂bgδbg))⊤Ri⊤Rj),rΔvij≐Ri⊤(vj−vi−gΔtij)−[Δv~ij(bˉig,bˉia)+∂Δvˉij∂bgδbg+∂Δvˉij∂baδba],rΔpij≐Ri⊤(pj−pi−viΔtij−12gΔtij2)−[Δpˉij(bˉig,bˉia)+∂Δpˉij∂bgδbg+∂Δpˉij∂baδba].\begin{align}\mathbf{r}_{\Delta \mathbf{R}_{ij}} &\doteq \text{Log}\left( \left( {\Delta \tilde{\mathbf{R}}}_{ij}(\bar{\mathbf{b}}_i^g) \text{Exp}\left( \frac{\partial \Delta \bar{\mathbf{R}}_{ij}}{\partial \mathbf{b}^g} \delta \mathbf{b}^g \right) \right)^\top \mathbf{R}_i^\top \mathbf{R}_j \right), \notag \\\mathbf{r}_{\Delta \mathbf{v}_{ij}} &\doteq \mathbf{R}_i^\top \left( \mathbf{v}_j - \mathbf{v}_i - \mathbf{g} \Delta t_{ij} \right) - \left[ \Delta \tilde{\mathbf{v}}_{ij}(\bar{\mathbf{b}}_i^g, \bar{\mathbf{b}}_i^a) + \frac{\partial \Delta \bar{\mathbf{v}}_{ij}}{\partial \mathbf{b}^g} \delta \mathbf{b}^g + \frac{\partial \Delta \bar{\mathbf{v}}_{ij}}{\partial \mathbf{b}^a} \delta \mathbf{b}^a \right], \notag \\\mathbf{r}_{\Delta \mathbf{p}_{ij}} &\doteq \mathbf{R}_i^\top \left( \mathbf{p}_j - \mathbf{p}_i - \mathbf{v}_i \Delta t_{ij} - \frac{1}{2} \mathbf{g} \Delta t_{ij}^2 \right) - \left[ \Delta \bar{\mathbf{p}}_{ij}(\bar{\mathbf{b}}_i^g, \bar{\mathbf{b}}_i^a) + \frac{\partial \Delta \bar{\mathbf{p}}_{ij}}{\partial \mathbf{b}^g} \delta \mathbf{b}^g + \frac{\partial \Delta \bar{\mathbf{p}}_{ij}}{\partial \mathbf{b}^a} \delta \mathbf{b}^a \right]. \tag{45}\end{align}
코드에서 구현된 IMU preintegration에 대한 Residual 함수는 EdgeInertial 클래스의 computeError 함수에 정의되어 있습니다. 여기서 끝부분에 있는 변수 er, ev, ep가 각각 rΔRij\mathbf{r}_{\Delta \mathbf{R}_{ij}}, rΔvij\mathbf{r}_{\Delta \mathbf{v}_{ij}}, rΔpij\mathbf{r}_{\Delta \mathbf{p}_{ij}}을 나타냅니다.
void EdgeInertial::computeError() { // TODO Maybe Reintegrate inertial measurments when difference between linearization point and current estimate is too big const VertexPose* VP1 = static_cast<const VertexPose*>(_vertices[0]); const VertexVelocity* VV1= static_cast<const VertexVelocity*>(_vertices[1]); const VertexGyroBias* VG1= static_cast<const VertexGyroBias*>(_vertices[2]); const VertexAccBias* VA1= static_cast<const VertexAccBias*>(_vertices[3]); const VertexPose* VP2 = static_cast<const VertexPose*>(_vertices[4]); const VertexVelocity* VV2 = static_cast<const VertexVelocity*>(_vertices[5]); const IMU::Bias b1(VA1->estimate()[0],VA1->estimate()[1],VA1->estimate()[2],VG1->estimate()[0],VG1->estimate()[1],VG1->estimate()[2]); const Eigen::Matrix3d dR = mpInt->GetDeltaRotation(b1).cast<double>(); const Eigen::Vector3d dV = mpInt->GetDeltaVelocity(b1).cast<double>(); const Eigen::Vector3d dP = mpInt->GetDeltaPosition(b1).cast<double>(); const Eigen::Vector3d er = LogSO3(dR.transpose()*VP1->estimate().Rwb.transpose()*VP2->estimate().Rwb); const Eigen::Vector3d ev = VP1->estimate().Rwb.transpose()*(VV2->estimate() - VV1->estimate() - g*dt) - dV; const Eigen::Vector3d ep = VP1->estimate().Rwb.transpose()*(VP2->estimate().twb - VP1->estimate().twb - VV1->estimate()*dt - g*dt*dt/2) - dP; _error << er, ev, ep; }
C++
복사
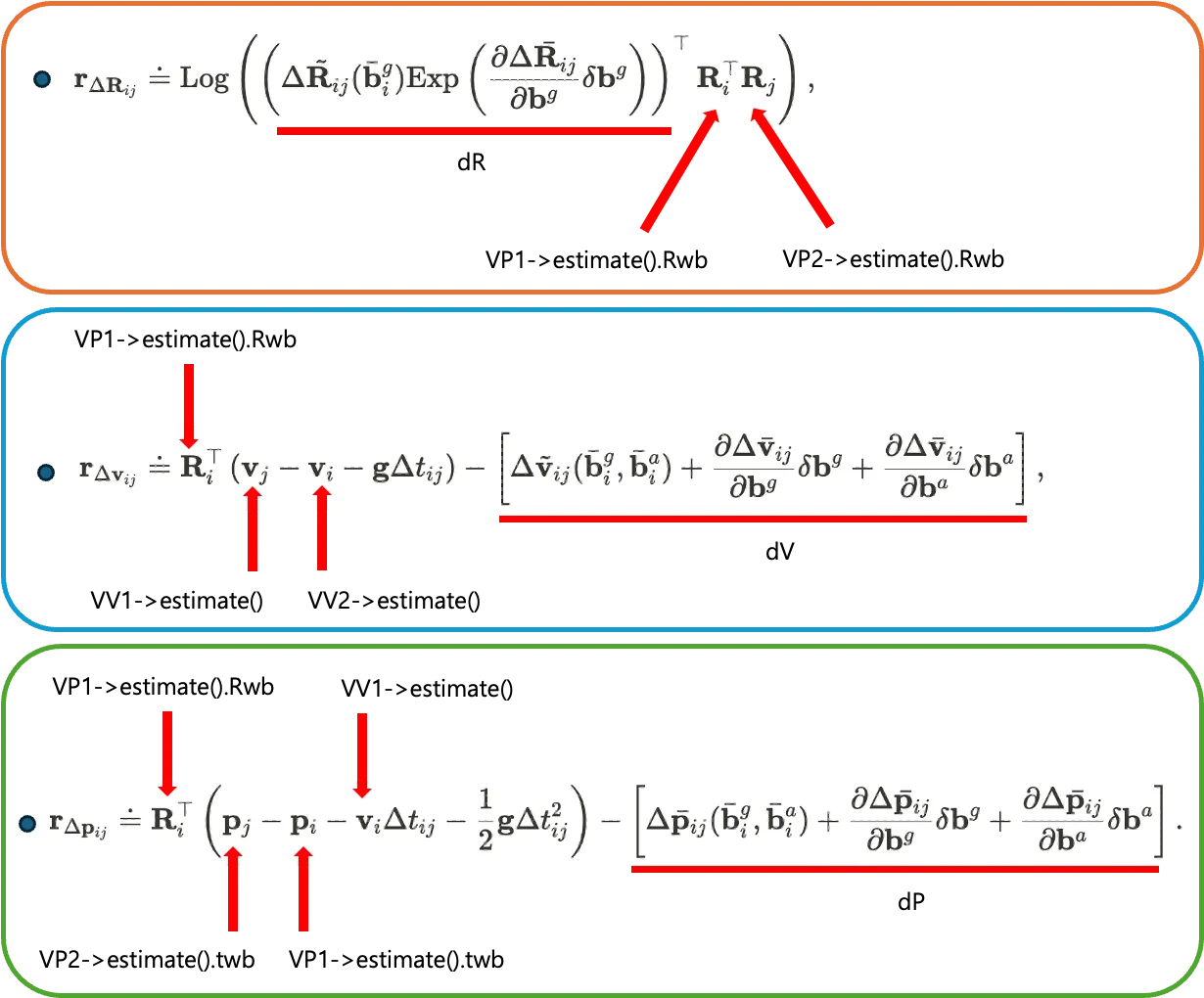
그림으로 대조하여 표현해보면 아래와 같습니다.
여기서 dR, dV, dP 변수들은 Residual 함수에서 시스템 상태에 대한 예측값으로 IMU 센서 데이터를 기반으로 연속된 두 시점 사이의 상태 변화를 적분하여 계산됩니다. 이 값들은 따로 함수로 구현되어 값을 얻게되는데 코드에서 dR, dV, dP 변수에 값이 대입되는 부분은 아래와 같습니다.
const Eigen::Matrix3d dR = mpInt->GetDeltaRotation(b1).cast<double>(); const Eigen::Vector3d dV = mpInt->GetDeltaVelocity(b1).cast<double>(); const Eigen::Vector3d dP = mpInt->GetDeltaPosition(b1).cast<double>();
C++
복사
함수 GetDeltaRotation, GetDeltaVelocity, GetDeltaPosition의 정의는 아래의 코드와 같고 수식 (45)에서 dR, dV, dP로 표시한 수식 부분과 동일하게 구현되어 있음을 확인할 수 있습니다. 여기서 JRg, JVg, JVa, JPg, JPa는 이전에 작성한 첫번째 글에서 살펴보았던 바이어스 업데이트를 위한 자코비안 행렬이 됩니다.
Eigen::Matrix3f Preintegrated::GetDeltaRotation(const Bias &b_) { std::unique_lock<std::mutex> lock(mMutex); Eigen::Vector3f dbg; dbg << b_.bwx-b.bwx,b_.bwy-b.bwy,b_.bwz-b.bwz; return NormalizeRotation(dR * Sophus::SO3f::exp(JRg * dbg).matrix()); } Eigen::Vector3f Preintegrated::GetDeltaVelocity(const Bias &b_) { std::unique_lock<std::mutex> lock(mMutex); Eigen::Vector3f dbg, dba; dbg << b_.bwx-b.bwx,b_.bwy-b.bwy,b_.bwz-b.bwz; dba << b_.bax-b.bax,b_.bay-b.bay,b_.baz-b.baz; return dV + JVg * dbg + JVa * dba; } Eigen::Vector3f Preintegrated::GetDeltaPosition(const Bias &b_) { std::unique_lock<std::mutex> lock(mMutex); Eigen::Vector3f dbg, dba; dbg << b_.bwx-b.bwx,b_.bwy-b.bwy,b_.bwz-b.bwz; dba << b_.bax-b.bax,b_.bay-b.bay,b_.baz-b.baz; return dP + JPg * dbg + JPa * dba; }
C++
복사
이렇게 구현된 Residual 함수는 IMU Preintegration을 수행할 때, 두 키프레임 사이의 상태 변화(회전, 속도, 위치)를 설명하는 IMU Factor 노드의 핵심 요소로 사용됩니다. Residual 함수는 예측값과 실제 상태 값 간의 오차를 정의하며, 이를 기반으로 최적화 식을 구성합니다. IMU 데이터를 적분하여 계산된 예측값과 실제 상태 변수 사이의 차이를 최소화함으로써, 최적화 과정은 시스템 상태 추정의 정밀도를 점진적으로 향상시키는데 사용됩니다.

Jacobian 행렬 정의

다음으로 Jacobian 행렬에 대해 살펴보겠습니다. Jacobian 행렬은 다변수 벡터 함수의 벡터 미분으로, 비선형 최적화 관점에서는 다변수 벡터 함수인 Residual 함수를 상태 변수로 미분한 결과를 의미합니다. 이를 통해 상태 변수가 변화할 때, 우리가 최소화해야 하는 Residual 함수가 어떻게 변화하는지를 나타냅니다. 따라서, Jacobian 행렬은 Residual 함수의 변화 방향과 크기를 나타내는 중요한 정보를 담고 있는 행렬이라고 이해할 수 있습니다.
IMU preintegration에 대한 Jacobian 행렬의 구현은 EdgeInertial 클래스의 linearizeOplus 함수에 구현이 되어있습니다. 코드에서는 편미분의 순서가 상태변수 기준으로 나열 되어 있고 논문에는 Residual 함수 기준으로 나열되어 있기 때문에 한눈에 파악하기가 어렵습니다. 따라서 코드에 대한 이해를 돕기 위해 기존의 ORB-SLAM3 코드에 // Comment (Dongwon Shin): 키워드로 부연 설명을 추가하였습니다.
void EdgeInertial::linearizeOplus() { const VertexPose* VP1 = static_cast<const VertexPose*>(_vertices[0]); const VertexVelocity* VV1= static_cast<const VertexVelocity*>(_vertices[1]); const VertexGyroBias* VG1= static_cast<const VertexGyroBias*>(_vertices[2]); const VertexAccBias* VA1= static_cast<const VertexAccBias*>(_vertices[3]); const VertexPose* VP2 = static_cast<const VertexPose*>(_vertices[4]); const VertexVelocity* VV2= static_cast<const VertexVelocity*>(_vertices[5]); const IMU::Bias b1(VA1->estimate()[0],VA1->estimate()[1],VA1->estimate()[2],VG1->estimate()[0],VG1->estimate()[1],VG1->estimate()[2]); const IMU::Bias db = mpInt->GetDeltaBias(b1); Eigen::Vector3d dbg; dbg << db.bwx, db.bwy, db.bwz; const Eigen::Matrix3d Rwb1 = VP1->estimate().Rwb; const Eigen::Matrix3d Rbw1 = Rwb1.transpose(); const Eigen::Matrix3d Rwb2 = VP2->estimate().Rwb; const Eigen::Matrix3d dR = mpInt->GetDeltaRotation(b1).cast<double>(); const Eigen::Matrix3d eR = dR.transpose()*Rbw1*Rwb2; const Eigen::Vector3d er = LogSO3(eR); const Eigen::Matrix3d invJr = InverseRightJacobianSO3(er); // Jacobians wrt Pose 1 _jacobianOplus[0].setZero(); // Comment (Dongwon Shin): derivative of rotation residual w.r.t rotation i _jacobianOplus[0].block<3,3>(0,0) = -invJr*Rwb2.transpose()*Rwb1; // OK // Comment (Dongwon Shin): derivative of velocity residual w.r.t rotation i _jacobianOplus[0].block<3,3>(3,0) = Sophus::SO3d::hat(Rbw1*(VV2->estimate() - VV1->estimate() - g*dt)); // OK // Comment (Dongwon Shin): derivative of translation residual w.r.t rotation i _jacobianOplus[0].block<3,3>(6,0) = Sophus::SO3d::hat(Rbw1*(VP2->estimate().twb - VP1->estimate().twb - VV1->estimate()*dt - 0.5*g*dt*dt)); // OK // translation // Comment (Dongwon Shin): derivative of translation residual w.r.t position i _jacobianOplus[0].block<3,3>(6,3) = -Eigen::Matrix3d::Identity(); // OK // Jacobians wrt Velocity 1 _jacobianOplus[1].setZero(); // Comment (Dongwon Shin): derivative of velocity residual w.r.t velocity i _jacobianOplus[1].block<3,3>(3,0) = -Rbw1; // OK // Comment (Dongwon Shin): derivative of translation residual w.r.t velocity i _jacobianOplus[1].block<3,3>(6,0) = -Rbw1*dt; // OK // Jacobians wrt Gyro 1 _jacobianOplus[2].setZero(); // Comment (Dongwon Shin): derivative of rotation residual w.r.t gyro bias i _jacobianOplus[2].block<3,3>(0,0) = -invJr*eR.transpose()*RightJacobianSO3(JRg*dbg)*JRg; // OK // Comment (Dongwon Shin): derivative of velocity residual w.r.t gyro bias i _jacobianOplus[2].block<3,3>(3,0) = -JVg; // OK // Comment (Dongwon Shin): derivative of translation residual w.r.t gyro bias i _jacobianOplus[2].block<3,3>(6,0) = -JPg; // OK // Jacobians wrt Accelerometer 1 _jacobianOplus[3].setZero(); // Comment (Dongwon Shin): derivative of velocity residual w.r.t acc bias i _jacobianOplus[3].block<3,3>(3,0) = -JVa; // OK // Comment (Dongwon Shin): derivative of translation residual w.r.t acc bias i _jacobianOplus[3].block<3,3>(6,0) = -JPa; // OK // Jacobians wrt Pose 2 _jacobianOplus[4].setZero(); // rotation // Comment (Dongwon Shin): derivative of rotation residual w.r.t rotation j _jacobianOplus[4].block<3,3>(0,0) = invJr; // OK // translation // Comment (Dongwon Shin): derivative of translation residual w.r.t position j _jacobianOplus[4].block<3,3>(6,3) = Rbw1*Rwb2; // OK // Jacobians wrt Velocity 2 _jacobianOplus[5].setZero(); // Comment (Dongwon Shin): derivative of velocity residual w.r.t velocity j _jacobianOplus[5].block<3,3>(3,0) = Rbw1; // OK }
C++
복사
IMU preintegration 논문에서는 Jacobian 행렬에 대한 수식 유도가 Appendix의 C. Jacobians of Residual Errors 섹션에 다음과 같이 설명되어 있습니다.
•
1) Jacobians of position residual rΔpij\mathbf{r}_{\Delta \mathbf{p}_{ij}}
∂rΔpij∂δϕi=(Ri⊤(pj−pi−viΔtij−12gΔtij2))∧,∂rΔpij∂δpi=−I3×1,∂rΔpij∂δvi=−Ri⊤Δtij,∂rΔpij∂δb~ia=−∂Δp~ij∂bia,∂rΔpij∂δϕj=0,∂rΔpij∂δpj=Ri⊤Rj,∂rΔpij∂δvj=0,∂rΔpij∂δb~ig=−∂Δp~ij∂big.\begin{aligned} \frac{\partial \mathbf{r}_{\Delta \mathbf{p}_{ij}}}{\partial \delta \boldsymbol{\phi}_i} &= \left( \mathbf{R}_i^\top \left( \mathbf{p}_j - \mathbf{p}_i - \mathbf{v}_i \Delta t_{ij} - \frac{1}{2} \mathbf{g} \Delta t_{ij}^2 \right) \right)^\wedge, \\ \frac{\partial \mathbf{r}_{\Delta \mathbf{p}_{ij}}}{\partial \delta \mathbf{p}_i} &= -\mathbf{I}_{3 \times 1}, \\ \frac{\partial \mathbf{r}_{\Delta \mathbf{p}_{ij}}}{\partial \delta \mathbf{v}_i} &= -\mathbf{R}_i^\top \Delta t_{ij}, \\ \frac{\partial \mathbf{r}_{\Delta \mathbf{p}_{ij}}}{\partial \delta \tilde{\mathbf{b}}_i^a} &= -\frac{\partial \Delta \tilde{\mathbf{p}}_{ij}}{\partial \mathbf{b}_i^a}, \end{aligned} \quad \begin{aligned} \frac{\partial \mathbf{r}_{\Delta \mathbf{p}_{ij}}}{\partial \delta \boldsymbol{\phi}_j} &= 0, \\ \frac{\partial \mathbf{r}_{\Delta \mathbf{p}_{ij}}}{\partial \delta \mathbf{p}_j} &= \mathbf{R}_i^\top \mathbf{R}_j, \\ \frac{\partial \mathbf{r}_{\Delta \mathbf{p}_{ij}}}{\partial \delta \mathbf{v}_j} &= 0, \\ \frac{\partial \mathbf{r}_{\Delta \mathbf{p}_{ij}}}{\partial \delta \tilde{\mathbf{b}}_i^g} &= -\frac{\partial \Delta \tilde{\mathbf{p}}_{ij}}{\partial \mathbf{b}_i^g}. \end{aligned}
•
2) Jacobians of velocity residual rΔvij\mathbf{r}_{\Delta \mathbf{v}_{ij}}
∂rΔvij∂δϕi=(Ri⊤(vj−vi−gΔtij))∧,∂rΔvij∂δpi=0,∂rΔvij∂δvi=−Ri⊤,∂rΔvij∂δb~ia=−∂Δv~ij∂bia,∂rΔvij∂δϕj=0,∂rΔvij∂δpj=0,∂rΔvij∂δvj=Ri⊤,∂rΔvij∂δb~ig=−∂Δv~ij∂big.\begin{aligned}\frac{\partial \mathbf{r}_{\Delta \mathbf{v}_{ij}}}{\partial \delta \boldsymbol{\phi}_i} &= \left( \mathbf{R}_i^\top \left( \mathbf{v}_j - \mathbf{v}_i - \mathbf{g} \Delta t_{ij} \right) \right)^\wedge, \\\frac{\partial \mathbf{r}_{\Delta \mathbf{v}_{ij}}}{\partial \delta \mathbf{p}_i} &= 0, \\\frac{\partial \mathbf{r}_{\Delta \mathbf{v}_{ij}}}{\partial \delta \mathbf{v}_i} &= -\mathbf{R}_i^\top, \\\frac{\partial \mathbf{r}_{\Delta \mathbf{v}_{ij}}}{\partial \delta \tilde{\mathbf{b}}_i^a} &= -\frac{\partial \Delta \tilde{\mathbf{v}}_{ij}}{\partial \mathbf{b}_i^a},\end{aligned}\quad\begin{aligned}\frac{\partial \mathbf{r}_{\Delta \mathbf{v}_{ij}}}{\partial \delta \boldsymbol{\phi}_j} &= 0, \\\frac{\partial \mathbf{r}_{\Delta \mathbf{v}_{ij}}}{\partial \delta \mathbf{p}_j} &= 0, \\\frac{\partial \mathbf{r}_{\Delta \mathbf{v}_{ij}}}{\partial \delta \mathbf{v}_j} &= \mathbf{R}_i^\top, \\\frac{\partial \mathbf{r}_{\Delta \mathbf{v}_{ij}}}{\partial \delta \tilde{\mathbf{b}}_i^g} &= -\frac{\partial \Delta \tilde{\mathbf{v}}_{ij}}{\partial \mathbf{b}_i^g}.\end{aligned}
•
3) Jacobians of rotation residual rΔRij\mathbf{r}_{\Delta \mathbf{R}_{ij}}
∂rΔRij∂δϕi=−Jr−1(rΔR(Ri))Rj⊤Ri,∂rΔRij∂δvi=0,∂rΔRij∂δpj=0,∂rΔRij∂δb~ia=0,∂rΔRij∂δpi=0,∂rΔRij∂δϕj=Jr−1(rΔR(Rj)),∂rΔRij∂δvj=0,∂rΔRij∂δb~ig=α.with α=−Jr−1(rΔRij(δbig))Exp(rΔRij(δbig))⊤Jrb∂ΔRˉij∂bg.\begin{aligned}\frac{\partial \mathbf{r}_{\Delta \mathbf{R}_{ij}}}{\partial \delta \boldsymbol{\phi}_i} &= -\mathbf{J}_r^{-1}(\mathbf{r}_{\Delta \mathbf{R}}(\mathbf{R}_i)) \mathbf{R}_j^\top \mathbf{R}_i, \\\frac{\partial \mathbf{r}_{\Delta \mathbf{R}_{ij}}}{\partial \delta \mathbf{v}_i} &= 0, \\\frac{\partial \mathbf{r}_{\Delta \mathbf{R}_{ij}}}{\partial \delta \mathbf{p}_j} &= 0, \\\frac{\partial \mathbf{r}_{\Delta \mathbf{R}_{ij}}}{\partial \delta \tilde{\mathbf{b}}_i^a} &= 0,\end{aligned}\quad\begin{aligned}\frac{\partial \mathbf{r}_{\Delta \mathbf{R}_{ij}}}{\partial \delta \mathbf{p}_i} &= 0, \\\frac{\partial \mathbf{r}_{\Delta \mathbf{R}_{ij}}}{\partial \delta \boldsymbol{\phi}_j} &= \mathbf{J}_r^{-1}(\mathbf{r}_{\Delta \mathbf{R}}(\mathbf{R}_j)), \\\frac{\partial \mathbf{r}_{\Delta \mathbf{R}_{ij}}}{\partial \delta \mathbf{v}_j} &= 0, \\\frac{\partial \mathbf{r}_{\Delta \mathbf{R}_{ij}}}{\partial \delta \tilde{\mathbf{b}}_i^g} &= \alpha.\end{aligned} \\\text{with } \alpha = -\mathbf{J}_r^{-1} \left( \mathbf{r}_{\Delta \mathbf{R}_{ij}}(\delta \mathbf{b}_i^g) \right) \text{Exp} \left( \mathbf{r}_{\Delta \mathbf{R}_{ij}}(\delta \mathbf{b}_i^g) \right)^\top \mathbf{J}_r^b \frac{\partial \Delta \bar{\mathbf{R}}_{ij}}{\partial \mathbf{b}^g}.
이는 회전, 속도, 이동에 대한 Residual 함수를 아래의 상태 변수에 대해 편미분한 결과를 정리한 것입니다.
•
키프레임 i에 대한 회전 상태 변수 ∂δϕi{\partial \delta \boldsymbol{\phi}_i}
•
키프레임 j에 대한 회전 상태 변수 ∂δϕj{\partial \delta \boldsymbol{\phi}_j}
•
키프레임 i에 대한 이동 상태 변수 ∂δpi{\partial \delta \mathbf{p}_i}
•
키프레임 j에 대한 회전 상태 변수 ∂δpj{\partial \delta \mathbf{p}_j}
•
키프레임 i에 대한 벡터 상태 변수 ∂δvi{\partial \delta \mathbf{v}_i}
•
키프레임 j에 대한 벡터 상태 변수 ∂δvj{\partial \delta \mathbf{v}_j}
•
키프레임 i에 대한 가속도 바이어스 상태 변수 ∂δb~ia{\partial \delta \tilde{\mathbf{b}}_i^a}
•
키프레임 i에 대한 각속도 바이어스 상태 변수 ∂δb~ig{\partial \delta \tilde{\mathbf{b}}_i^g}
예를 들어 아래에 표시한 Jacobian 행렬 코드에서 derivative of rotation residual w.r.t rotation i는 회전 Residual 함수 rΔRij\mathbf{r}_{\Delta \mathbf{R}_{ij}} 에 대해 키프레임 i에서의 회전 상태변수 ∂δϕi{\partial \delta \boldsymbol{\phi}_i}로 편미분한 결과로 생각하면 돼고 이는 논문에서 ∂rΔRij∂δϕi\frac{\partial \mathbf{r}_{\Delta \mathbf{R}_{ij}}}{\partial \delta \boldsymbol{\phi}_i}를 의미합니다.
// Comment (Dongwon Shin): derivative of rotation residual w.r.t rotation i _jacobianOplus[0].block<3,3>(0,0) = -invJr*Rwb2.transpose()*Rwb1; // OK
C++
복사
∂rΔRij∂δϕi=−Jr−1(rΔR(Ri))Rj⊤Ri\frac{\partial \mathbf{r}_{\Delta \mathbf{R}_{ij}}}{\partial \delta \boldsymbol{\phi}_i} = -\mathbf{J}_r^{-1}(\mathbf{r}_{\Delta \mathbf{R}}(\mathbf{R}_i)) \mathbf{R}_j^\top \mathbf{R}_i
이와 같은 방식으로 논문과 코드를 대조해보면 논문의 Jacobian 행렬에 대한 수식이 그대로 구현되어 있음을 확인할 수 있습니다.

마무리

처음에는 ORB-SLAM3에는 IMU preintegration이 어떻게 실제로 구현되어 있을까에 대한 궁금증으로 시작해서 자료를 찾다가 없어서 직접 설명하는 글을 써보기까지 했네요 ㅎ 홈페이지에 블로그 글을 올리는 것은 굉장히 오랜만이었는데 앞으로는 종종 공부하는 내용을 정리해서 올려볼까 합니다 ㅎ 공부하다 보니 또 다른 대표적인 Visual inertial odometry 방법인 VINS-MONO에서는 ORB-SLAM3와는 다른 방식으로 IMU preintegration을 수행하는 것을 발견해서 다음에는 해당 내용으로 한번 글을 써볼까합니다. 최근에 진행했던 Semantic SLAM이나 Deep learning based visual localization 쪽도 기회가 된다면 한번 써보도록 하겠습니다 ㅎ
평소에 IMU 센서 퓨전 쪽에 관심만 가지고 있다가 이번 기회에 IMU preintegration 쪽을 공부하면서 조금 더 친해진 느낌이네요 ㅎ 최근 애플에서도 비전프로와 같은 메타버스 기기를 만들기 위해 VIO/SLAM 엔지니어를 채용하고 있는데, 자율주행, 로보틱스와 더불어 점점 더 사용되는 분야가 많아지는 느낌입니다 ㅎ
끝까지 읽어주셔서 감사합니다 :-)