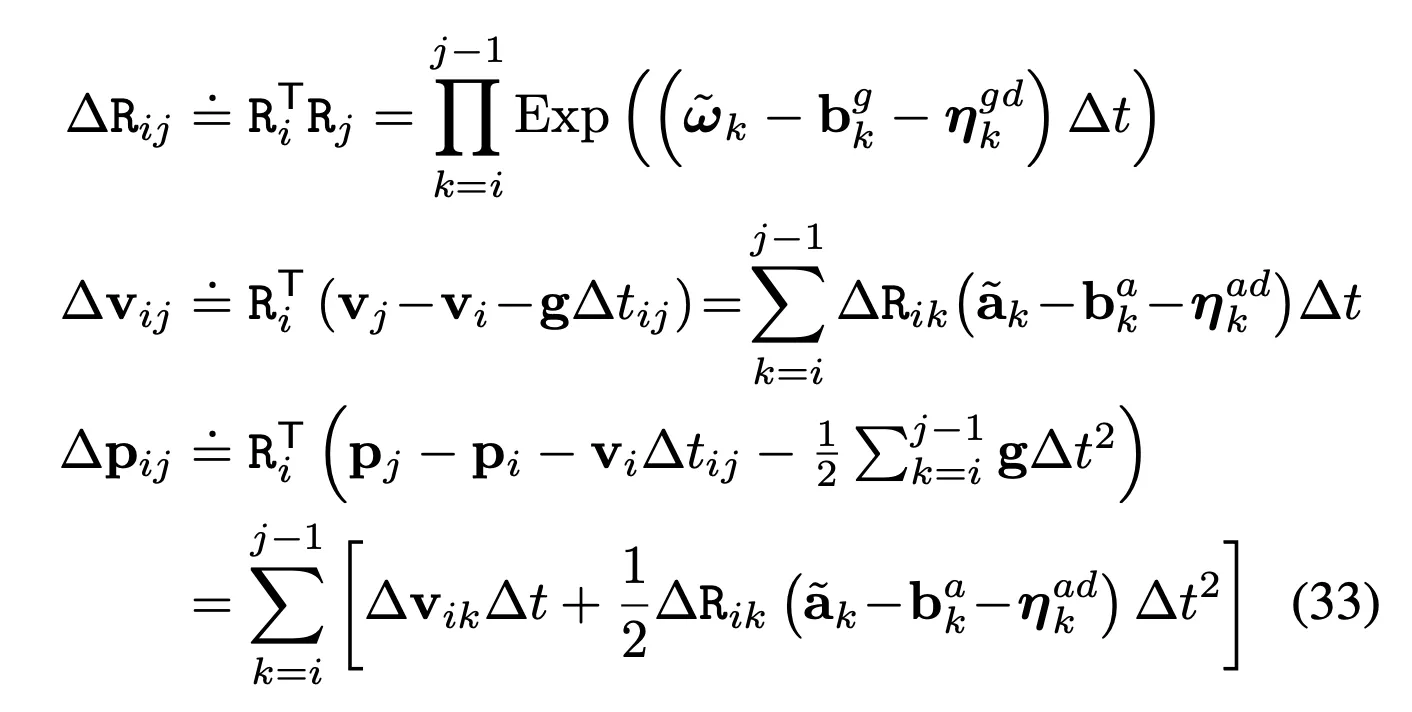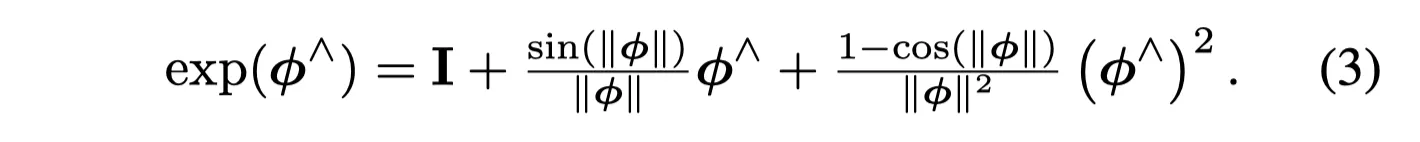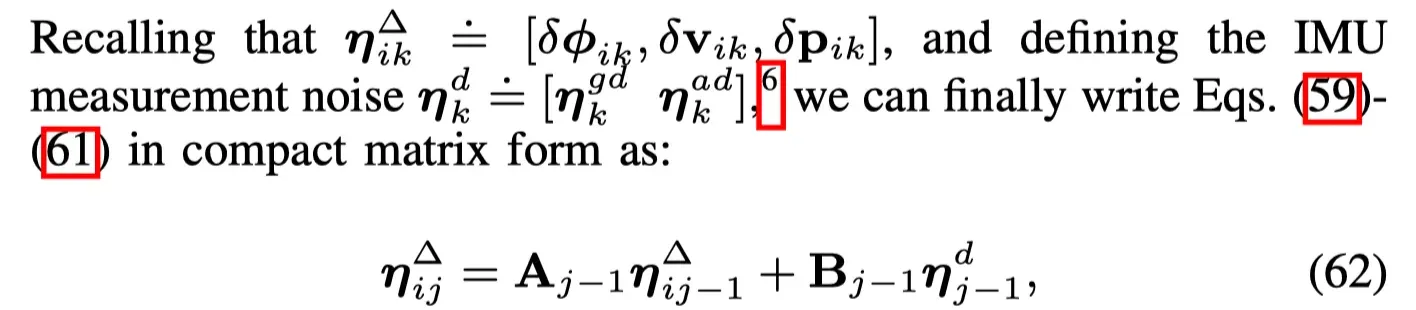ORB-SLAM3 IMU preintegration code review (1)

날짜
2025/01/05
4 more properties

소개

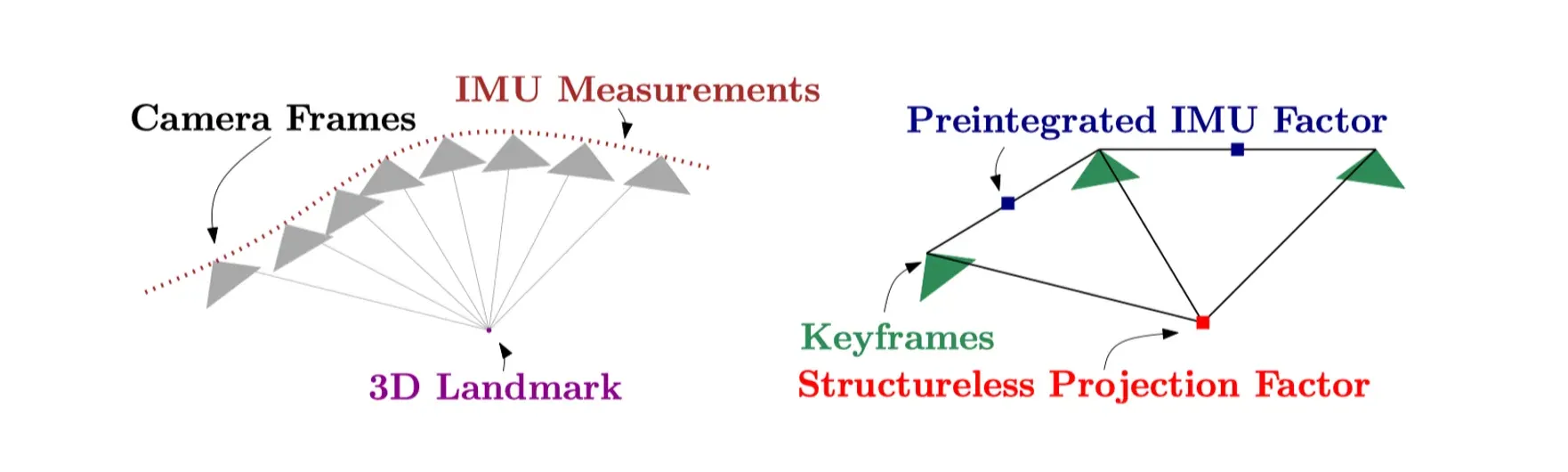
최근 IMU preintegration에 대해서 공부하다가 문득 ORB-SLAM3는 어떻게 IMU preintegration이 구현되어 있을지 궁금해서 분석해보았습니다. IMU preintegration에 대한 이론적인 부분은 형태님의 블로그에 이미 잘 설명이 되어있기 때문에 그 쪽을 참고하시면 좋을것 같고 저는 IMU preintegration 논문과 ORB-SLAM3 코드를 대조해보면서 논문의 수식이 코드에서 어떻게 구현되어 있는지를 살펴보았습니다.
Imu preintegration 부분을 하나의 글로 다 써내려가기는 시간이 많이 걸릴거 같아서 아래와 같은 순서의 글로 작성하고자합니다.
1.
IMU 센서 측정 값 integration
2.
Residual 함수 정의
3.
Jacobian 행렬 정의
본 글에서는 그 중 첫번째인 IMU 센서 측정값 integration에 대한 코드 분석 내용을 다룹니다.

코드 분석

IMU 센서 측정 값 integration

먼저 IMU 센서로부터 가속도 및 각속도 측정값이 들어오면 누적하여 키프레임 i와 키프레임 j사이의 measurements를 integration하는 부분에 대해서 살펴보도록 하겠습니다. 이 과정에서 아래와 같은 값들이 계산됩니다.
1.
두 키프레임 사이의 상대적인 상태(회전, 이동, 속도) 값
2.
노이즈 전파를 통해 나중에 최적화를 수행할때 사용되는 공분산 행렬
3.
바이어스 업데이트를 위한 자코비안 행렬
전체적인 계산은 Preintegrated 클래스의 IntegrateNewMeasurement 함수에서 수행됩니다. 전체 함수 코드를 살펴보면 아래와 같습니다.
void Preintegrated::IntegrateNewMeasurement(const Eigen::Vector3f &acceleration, const Eigen::Vector3f &angVel, const float &dt) { mvMeasurements.push_back(integrable(acceleration,angVel,dt)); // Position is updated firstly, as it depends on previously computed velocity and rotation. // Velocity is updated secondly, as it depends on previously computed rotation. // Rotation is the last to be updated. //Matrices to compute covariance Eigen::Matrix<float,9,9> A; A.setIdentity(); Eigen::Matrix<float,9,6> B; B.setZero(); Eigen::Vector3f acc, accW; acc << acceleration(0)-b.bax, acceleration(1)-b.bay, acceleration(2)-b.baz; accW << angVel(0)-b.bwx, angVel(1)-b.bwy, angVel(2)-b.bwz; avgA = (dT*avgA + dR*acc*dt)/(dT+dt); avgW = (dT*avgW + accW*dt)/(dT+dt); // Update delta position dP and velocity dV (rely on no-updated delta rotation) dP = dP + dV*dt + 0.5f*dR*acc*dt*dt; dV = dV + dR*acc*dt; // Compute velocity and position parts of matrices A and B (rely on non-updated delta rotation) Eigen::Matrix<float,3,3> Wacc = Sophus::SO3f::hat(acc); A.block<3,3>(3,0) = -dR*dt*Wacc; A.block<3,3>(6,0) = -0.5f*dR*dt*dt*Wacc; A.block<3,3>(6,3) = Eigen::DiagonalMatrix<float,3>(dt, dt, dt); B.block<3,3>(3,3) = dR*dt; B.block<3,3>(6,3) = 0.5f*dR*dt*dt; // Update position and velocity jacobians wrt bias correction JPa = JPa + JVa*dt -0.5f*dR*dt*dt; JPg = JPg + JVg*dt -0.5f*dR*dt*dt*Wacc*JRg; JVa = JVa - dR*dt; JVg = JVg - dR*dt*Wacc*JRg; // Update delta rotation IntegratedRotation dRi(angVel,b,dt); dR = NormalizeRotation(dR*dRi.deltaR); // Compute rotation parts of matrices A and B A.block<3,3>(0,0) = dRi.deltaR.transpose(); B.block<3,3>(0,0) = dRi.rightJ*dt; // Update covariance C.block<9,9>(0,0) = A * C.block<9,9>(0,0) * A.transpose() + B*Nga*B.transpose(); C.block<6,6>(9,9) += NgaWalk; // Update rotation jacobian wrt bias correction JRg = dRi.deltaR.transpose()*JRg - dRi.rightJ*dt; // Total integrated time dT += dt; }
C++
복사
전체적으로 보면 계산하는 부분이 뒤죽박죽 섞여있어서 한눈에 파악하기가 힘드므로 위에서 언급한 3가지 부분에 대해서 순서대로 살펴보도록 하겠습니다.

Relative motion increments

Imu preintegration 논문에서 수식 (33)을 보면 relative motion increments에 대한 수식이 정의되어 있습니다.
먼저 relative motion increments 중에 위치(position)에 대한 항 Δpij≐∑k=ij−1[ΔvikΔt+12ΔRik(a~k−bka−ηkad)Δt2]\Delta \mathbf{p}_{ij} \doteq \sum_{k=i}^{j-1} \left[ \Delta \mathbf{v}_{ik} \Delta t + \frac{1}{2} \Delta \mathbf{R}_{ik} \left( \tilde{\mathbf{a}}_k - \mathbf{b}^a_k - \boldsymbol{\eta}^{ad}_k \right) \Delta t^2 \right]을 코드에서 찾아보면 아래와 같습니다.
dP = dP + dV*dt + 0.5f*dR*acc*dt*dt;
C++
복사
여기서 acc는 바이어스 bka\mathbf{b}^a_k가 제거된 형태의 가속도 값을 나타냅니다. 노이즈 ηkad\boldsymbol{\eta}^{ad}_k는 따로 모델링 되어 공분산행렬을 만드는데 사용되기 때문에 여기서는 고려하지 않아도 됩니다. 그리고 합을 나타내는 Σ\Sigma 기호는 코드에서 dP = dP + something 형태로 표현된 것을 알 수 있습니다.
다음으로 속도(velocity)에 대한 항 Δvij≐∑k=ij−1ΔRik(a~k−bka−ηkad)Δt\Delta \mathbf{v}_{ij} \doteq \sum_{k=i}^{j-1} \Delta \mathbf{R}{ik} \left( \tilde{\mathbf{a}}_k - \mathbf{b}^a_k - \boldsymbol{\eta}^{ad}_k \right) \Delta t을 코드에서 찾아보면 아래와 같습니다. 여기서 acc도 마찬가지로 위에서 언급한 표현으로 생각하시면 됩니다.
dV = dV + dR*acc*dt;
C++
복사
다음으로 회전(rotation)에 대한 항 ΔRij≐Ri⊤Rj=∏k=ij−1Exp((ω~k−bkg−ηkgd)Δt)\Delta \mathbf{R}_{ij} \doteq \mathbf{R}_i^\top \mathbf{R}_j = \prod_{k=i}^{j-1} \mathrm{Exp} \left( \left( \tilde{\boldsymbol{\omega}}_k - \mathbf{b}^g_k - \boldsymbol{\eta}^{gd}_k \right) \Delta t \right)을 코드에서 찾아보면 아래와 같습니다.
IntegratedRotation dRi(angVel,b,dt); dR = NormalizeRotation(dR*dRi.deltaR);
C++
복사
이 부분은 논문의 코드와는 조금 달라보이는데 여기서 IntegratedRotation 클래스의 생성자 부분을 살펴보면 논문의 수식이 작성되어 있음을 알 수 있습니다.
IntegratedRotation::IntegratedRotation(const Eigen::Vector3f &angVel, const Bias &imuBias, const float &time) { const float x = (angVel(0)-imuBias.bwx)*time; const float y = (angVel(1)-imuBias.bwy)*time; const float z = (angVel(2)-imuBias.bwz)*time; const float d2 = x*x+y*y+z*z; const float d = sqrt(d2); Eigen::Vector3f v; v << x, y, z; Eigen::Matrix3f W = Sophus::SO3f::hat(v); if(d<eps) { deltaR = Eigen::Matrix3f::Identity() + W; rightJ = Eigen::Matrix3f::Identity(); } else { deltaR = Eigen::Matrix3f::Identity() + W*sin(d)/d + W*W*(1.0f-cos(d))/d2; rightJ = Eigen::Matrix3f::Identity() - W*(1.0f-cos(d))/d2 + W*W*(d-sin(d))/(d2*d); } }
C++
복사
여기서 수식의 (ω~k−bkg−ηkgd)\left( \tilde{\boldsymbol{\omega}}_k - \mathbf{b}^g_k - \boldsymbol{\eta}^{gd}_k \right)부분은 아래 코드 부분이고
const float x = (angVel(0)-imuBias.bwx)*time; const float y = (angVel(1)-imuBias.bwy)*time; const float z = (angVel(2)-imuBias.bwz)*time;
C++
복사
Exponential map을 나타내는 Exp()\mathrm{Exp}()함수가 작성된 부분은 아래 코드 부분입니다.
Eigen::Matrix3f W = Sophus::SO3f::hat(v); if(d<eps) { deltaR = Eigen::Matrix3f::Identity() + W; rightJ = Eigen::Matrix3f::Identity(); } else { deltaR = Eigen::Matrix3f::Identity() + W*sin(d)/d + W*W*(1.0f-cos(d))/d2; rightJ = Eigen::Matrix3f::Identity() - W*(1.0f-cos(d))/d2 + W*W*(d-sin(d))/(d2*d); }
C++
복사
Exponential map은 논문에서 수식 (3)에서 잘 설명하고 있습니다.
이러한 항들을 이용해서 지속적으로 들어오는 IMU 센서의 가속도 및 각속도 값을 누적하여 키프레임 i와 j사이의 relative motion을 예측할 수 있게 됩니다. 이러한 relative motion은 나중에 키프레임들을 이용한 Bundle adjustment를 수행할 때나, 카메라 프레임 하나에 대한 Pose estimation을 수행할 때 사용하게 됩니다.

Covariance from noise propagation

다음으로 노이즈 전파를 위해 논문의 수식 (62)에서 이야기하는 행렬 A와 B가 필요합니다.
ηijΔ=Aj−1ηij−1Δ+Bj−1ηj−1d,(62)\boldsymbol{\eta}_{ij}^\Delta = \mathbf{A}_{j-1} \boldsymbol{\eta}_{ij-1}^\Delta + \mathbf{B}_{j-1} \boldsymbol{\eta}_{j-1}^d, \tag{62}
그런데 논문에서는 행렬 A와 B가 명시적으로 어떻게 구성되었다고 나타내고 있지는 않습니다. 대신 논문에서는 아래와 같이 이야기 하고 있습니다.
따라서 ηijΔ\boldsymbol{\eta}_{ij}^\Delta와 ηj−1d\boldsymbol{\eta}_{j-1}^d의 정의에 의해 수식 (59)-(61)로부터 [δϕij−1,δvij−1,δpij−1][\delta \boldsymbol{\phi}_{ij-1}, \delta \mathbf{v}_{ij-1}, \delta \mathbf{p}_{ij-1}]와 [ηj−1gd,ηj−1ad][\boldsymbol{\eta}_{j-1}^{gd}, \boldsymbol{\eta}_{j-1}^{ad}]항이 곱해지는 계수항들을 따로 모아서 정리해보면 아래와 같습니다.
[δϕijδvijδpij]=[ΔR~j−1j⊤00−ΔR~ij−1(a~j−1−bia)ΔtI0−12ΔR~ij−1(a~j−1−bia)Δt2ΔtII][δϕij−1δvij−1δpij−1]+[Jrj−100ΔR~ij−1Δt012ΔR~ij−1Δt2][ηj−1gdηj−1ad]\begin{bmatrix}\delta \boldsymbol{\phi}_{ij} \\\delta \mathbf{v}_{ij} \\\delta \mathbf{p}_{ij}\end{bmatrix}=\begin{bmatrix}\Delta \tilde{\mathbf{R}}_{j-1j}^\top & \mathbf{0} & \mathbf{0} \\-\Delta \tilde{\mathbf{R}}_{ij-1} \left( \tilde{\mathbf{a}}_{j-1} - \mathbf{b}^a_i \right) \Delta t & \mathbf{I} & \mathbf{0} \\-\frac{1}{2} \Delta \tilde{\mathbf{R}}_{ij-1} \left( \tilde{\mathbf{a}}_{j-1} - \mathbf{b}^a_i \right) \Delta t^2 & \Delta t \mathbf{I} & \mathbf{I}\end{bmatrix}\begin{bmatrix}\delta \boldsymbol{\phi}_{ij-1} \\\delta \mathbf{v}_{ij-1} \\\delta \mathbf{p}_{ij-1}\end{bmatrix}+\begin{bmatrix}\mathbf{J}_{r}^{j-1} & \mathbf{0} \\\mathbf{0} & \Delta \tilde{\mathbf{R}}_{ij-1} \Delta t \\\mathbf{0} & \frac{1}{2}\Delta \tilde{\mathbf{R}}_{ij-1} \Delta t^2\end{bmatrix}\begin{bmatrix}\boldsymbol{\eta}_{j-1}^{gd} \\\boldsymbol{\eta}_{j-1}^{ad}\end{bmatrix}
정리된 수식에서 행렬 A와 B에 해당하는 부분을 코드에서 찾아보면
// Compute velocity and position parts of matrices A and B (rely on non-updated delta rotation) Eigen::Matrix<float,3,3> Wacc = Sophus::SO3f::hat(acc); A.block<3,3>(3,0) = -dR*dt*Wacc; A.block<3,3>(6,0) = -0.5f*dR*dt*dt*Wacc; A.block<3,3>(6,3) = Eigen::DiagonalMatrix<float,3>(dt, dt, dt); B.block<3,3>(3,3) = dR*dt; B.block<3,3>(6,3) = 0.5f*dR*dt*dt; (...) // Compute rotation parts of matrices A and B A.block<3,3>(0,0) = dRi.deltaR.transpose(); B.block<3,3>(0,0) = dRi.rightJ*dt;
C++
복사
행렬 A와 B를 대조해보면 논문과 동일하게 코드가 작성되어 있는 것을 확인할 수 있습니다.
행렬 A와 B가 정리되었다면 이제 공분산 행렬을 구할수 있습니다.
Σij=Aj−1Σij−1Aj−1⊤+Bj−1ΣηBj−1⊤(63)\Sigma_{ij} = \mathbf{A}_{j-1} \Sigma_{ij-1} \mathbf{A}_{j-1}^\top + \mathbf{B}_{j-1} \Sigma_{\eta} \mathbf{B}_{j-1}^\top \tag{63}
// Update covariance C.block<9,9>(0,0) = A * C.block<9,9>(0,0) * A.transpose() + B*Nga*B.transpose(); C.block<6,6>(9,9) += NgaWalk;
C++
복사
여기서 공분산 행렬을 나타내는 Σ\Sigma기호는 코드에서 C로 표현된 것을 알 수 있습니다.

Jacobians used for the a bias update

다음으로 바이어스 업데이트를 위한 자코비안을 계산해야합니다. 이 부분은 논문에서 수식번호가 따로 없고 Appendix에서 수식 (70)번 위에 위치하고 있습니다. 이는 Residual 함수를 가속도 및 각속도 바이어스 항으로 편미분한 결과를 의미합니다.
∂ΔRˉij∂bg=−∑k=ij−1[ΔR~k+1:j(bˉi)⊤JrkΔt],∂Δvˉij∂ba=−∑k=ij−1ΔRˉikΔt,∂Δvˉij∂bg=−∑k=ij−1ΔRˉik(a~k−bˉia)∧∂ΔRˉik∂bgΔt,∂Δpˉij∂bg=∑k=ij−1∂Δvˉik∂bgΔt−12ΔRˉikΔt2,∂Δpˉij∂ba=∑k=ij−1∂Δvˉik∂baΔt−12ΔRˉik(a~k−bˉia)∧∂ΔRˉik∂bgΔt2.\begin{aligned}\frac{\partial \Delta \bar{\mathbf{R}}_{ij}}{\partial \mathbf{b}^g} &=- \sum_{k=i}^{j-1} \left[ \Delta \tilde{\mathbf{R}}_{k+1:j} (\bar{\mathbf{b}}_i)^\top \mathbf{J}_r^k \Delta t \right], \\\frac{\partial \Delta \bar{\mathbf{v}}_{ij}}{\partial \mathbf{b}^a} &=- \sum_{k=i}^{j-1} \Delta \bar{\mathbf{R}}_{ik} \Delta t, \\\frac{\partial \Delta \bar{\mathbf{v}}_{ij}}{\partial \mathbf{b}^g} &=- \sum_{k=i}^{j-1} \Delta \bar{\mathbf{R}}_{ik} \left( \tilde{\mathbf{a}}_k - \bar{\mathbf{b}}_i^a \right)^\wedge \frac{\partial \Delta \bar{\mathbf{R}}_{ik}}{\partial \mathbf{b}^g} \Delta t, \\\frac{\partial \Delta \bar{\mathbf{p}}_{ij}}{\partial \mathbf{b}^g} &=\sum_{k=i}^{j-1} \frac{\partial \Delta \bar{\mathbf{v}}_{ik}}{\partial \mathbf{b}^g} \Delta t - \frac{1}{2} \Delta \bar{\mathbf{R}}_{ik} \Delta t^2, \\\frac{\partial \Delta \bar{\mathbf{p}}_{ij}}{\partial \mathbf{b}^a} &=\sum_{k=i}^{j-1} \frac{\partial \Delta \bar{\mathbf{v}}_{ik}}{\partial \mathbf{b}^a} \Delta t - \frac{1}{2} \Delta \bar{\mathbf{R}}_{ik} \left( \tilde{\mathbf{a}}_k - \bar{\mathbf{b}}_i^a \right)^\wedge \frac{\partial \Delta \bar{\mathbf{R}}_{ik}}{\partial \mathbf{b}^g} \Delta t^2.\end{aligned}
// Update position and velocity jacobians wrt bias correction JPa = JPa + JVa*dt -0.5f*dR*dt*dt; JPg = JPg + JVg*dt -0.5f*dR*dt*dt*Wacc*JRg; JVa = JVa - dR*dt; JVg = JVg - dR*dt*Wacc*JRg; (...) // Update rotation jacobian wrt bias correction JRg = dRi.deltaR.transpose()*JRg - dRi.rightJ*dt;
C++
복사
여기서 JPa는 ∂Δpˉij∂ba\frac{\partial \Delta \bar{\mathbf{p}}_{ij}}{\partial \mathbf{b}^a}, JPg는 ∂Δpˉij∂bg\frac{\partial \Delta \bar{\mathbf{p}}_{ij}}{\partial \mathbf{b}^g}, JVa는 ∂Δvˉij∂ba\frac{\partial \Delta \bar{\mathbf{v}}_{ij}}{\partial \mathbf{b}^a}, JVg는 ∂Δvˉij∂bg\frac{\partial \Delta \bar{\mathbf{v}}_{ij}}{\partial \mathbf{b}^g}, JRg는 ∂ΔRˉij∂bg\frac{\partial \Delta \bar{\mathbf{R}}_{ij}}{\partial \mathbf{b}^g}를 나타냅니다. 보시면 회전값은 각속도 바이어스에 대해서만 영향을 받으므로 각속도 바이어스에 대한 편미분만 수행합니다. 하지만 속도와 위치값은 가속도 및 각속도 바이어스에 대해서 모두 영향을 받으므로 두 항에 대해 모두 편미분을 수행합니다.
여기 자코비안 행렬들은 나중에 설명할 residual error를 구할때 사용하게 됩니다.

마무리

일단 여기까지 해서 ORB-SLAM3 코드의 imu preintegration에서 첫번째인 IMU 센서 측정 값 integration의 구현이 어떻게 되어있는지를 살펴보았습니다. 측정값 integration부분에서는 (1) 두 키프레임 사이의 상대적인 상태 (회전, 이동, 속도) 값을 계산하고, (2) 노이즈 전파를 통해 최적화를 수행할때 사용되는 공분산 행렬을 구합니다. 또한 (3) 바이어스 업데이트를 위한 자코비안 행렬을 계산하여 이 값들을 나중에 키프레임들을 이용한 Bundle adjustment를 수행할 때나, 카메라 프레임 하나에 대한 Pose estimation을 수행할 때 사용합니다.
다음시간에는 이렇게 정의된 relative motion increments값을 이용해 두 키프레임 사이의 residual 함수를 정의하고 이를 최적화 시키는데 사용하는 Jacobian 행렬이 어떻게 구현되어 있는지 논문과 대조하여 살펴보도록 하겠습니다.
긴 글 읽어주셔서 감사합니다 :-)